函數>函數的遞迴使用
函數的遞迴使用
一個函數在它的函數體內使用它自身稱為遞迴使用。這種函數稱為遞迴函數。C語言允許函數的遞迴使用。在遞迴使用中,主調函數又是被調函數。執行遞迴函數將反復使用其自身,每使用一次就進入新的一層。
例如有函數f如下:
|
int f(int x) { int y; z=f(y); return z; } |
這個函數是一個遞迴函數。但是運行該函數將無休止地使用其自身,這當然是不正確的。為了防止遞迴使用無終止地進行,必須在函數內有終止遞迴使用的手段。常用的辦法是加條件判斷,滿足某種條件後就不再作遞迴使用,然後逐層返回。下面舉例說明遞迴使用的執行過程。
【例】用遞迴法計算n!
用遞迴法計算n!可用下述公式表示:
n!=1 (n=0,1)
n×(n-1)! (n>1)
按公式可編程如下:
|
long ff(int n) { long f; if(n<0) printf("n<0,input error"); else if(n==0||n==1) f=1; else f=ff(n-1)*n; return(f); } main() { int n; long y; printf("\ninput a inteager number:\n"); scanf("%d",&n); y=ff(n); printf("%d!=%ld",n,y); } |
|
|
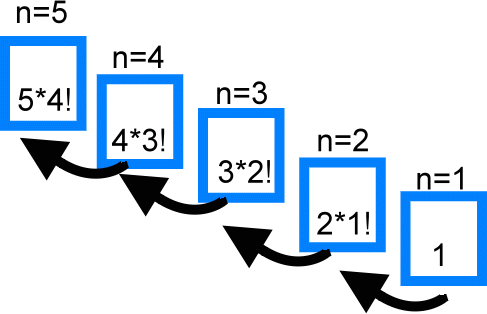
程式中給出的函數ff是一個遞迴函數。主函數使用ff 後即進入函數ff執行,如果n<0,n==0或n=1時都將結束函數的執行,否則就遞迴使用ff函數自身。由於每次遞迴使用的實參為n-1,即把n-1的值賦予形參n,最後當n-1的值為1時再作遞迴使用,形參n的值也為1,將使遞迴終止。然後可逐層退回。
下面我們再舉例說明該過程。設執行本程式時輸入為5,即求5!。在主函數中的使用語句即為y=ff(5),進入ff函數後,由於n=5,不等於0或1,故應執行f=ff(n-1)*n,即f=ff(5-1)*5。該語句對ff作遞迴使用即ff(4)。
進行四次遞迴使用後,ff函數形參取得的值變為1,故不再繼續遞迴使用而開始逐層返回主調函數。ff(1)的函數返回值為1,ff(2)的返回值為1*2=2,ff(3)的返回值為2*3=6,ff(4)的返回值為6*4=24,最後返回值ff(5)為24*5=120。
例8.5也可以不用遞迴的方法來完成。如可以用遞推法,即從1開始乘以2,再乘以3…直到n。遞推法比遞迴法更容易理解和實現。但是有些問題則只能用遞迴演算法才能實現。典型的問題是Hanoi塔問題。
【例】河內塔(Hanoi塔)問題
一塊板上有三根針,A,B,C。A針上套有64個大小不等的圓盤,大的在下,小的在上。如圖5.4所示。要把這64個圓盤從A針移動C針上,每次只能移動一個圓盤,移動可以借助B針進行。但在任何時候,任何針上的圓盤都必須保持大盤在下,小盤在上。求移動的步驟。
|
本題演算法分析如下,設A上有n個盤子。 如果n=1,則將圓盤從A直接移動到C。 如果n=2,則: 1.將A上的n-1(等於1)個圓盤移到B上; 2.再將A上的一個圓盤移到C上; 3.最後將B上的n-1(等於1)個圓盤移到C上。 如果n=3,則: A. 將A上的n-1(等於2,令其為n`)個圓盤移到B(借助於C),步驟如下: (1)將A上的n`-1(等於1)個圓盤移到C上。 (2)將A上的一個圓盤移到B。 (3)將C上的n`-1(等於1)個圓盤移到B。 B. 將A上的一個圓盤移到C。 C. 將B上的n-1(等於2,令其為n`)個圓盤移到C(借助A),步驟如下: (1)將B上的n`-1(等於1)個圓盤移到A。 (2)將B上的一個盤子移到C。 (3)將A上的n`-1(等於1)個圓盤移到C。 到此,完成了三個圓盤的移動過程。 從上面分析可以看出,當n大於等於2時,移動的過程可分解為三個步驟: 第一步 把A上的n-1個圓盤移到B上; 第二步 把A上的一個圓盤移到C上; 第三步 把B上的n-1個圓盤移到C上;其中第一步和第三步是類同的。
當n=3時,第一步和第三步又分解為類同的三步,即把n`-1個圓盤從一個針移到另一個針上,這裏的n`=n-1。 |
顯然這是一個遞迴過程,據此演算法可編程如下:
|
#include<stdio.h> move(int n,int x,int y,int z) { if(n==1) printf("%c-->%c\n",x,z); else { move(n-1,x,z,y); printf("%c-->%c\n",x,z); move(n-1,y,x,z); } } main() { int h; printf("\ninput number:\n"); scanf("%d",&h); printf("the step to moving %2d diskes:\n",h); move(h,'a','b','c'); }
|
從程式中可以看出,move函數是一個遞迴函數,它有四個形參n,x,y,z。n表示圓盤數,x,y,z分別表示三根針。move 函數的功能是把x上的n個圓盤移動到z上。當n==1時,直接把x上的圓盤移至z上,輸出x→z。如n!=1則分為三步:遞迴使用move函數,把n-1個圓盤從x移到y;輸出x→z;遞迴使用move函數,把n-1個圓盤從y移到z。在遞迴使用過程中n=n-1,故n的值逐次遞減,最後n=1時,終止遞迴,逐層返回。當n=4 時程式運行的結果為:
input number:
4
the step to moving 4 diskes:
a→b
a→c
b→c
a→b
c→a
c→b
a→b
a→c
b→c
b→a
c→a
b→c
a→b
a→c
b→c