遞迴

遞迴的定義:一個函式呼叫自己本身.

至少要定義2種條件:

什麼情況下作遞迴（呼叫自己）
什麼情況下作遞迴結束

階乘問題

由 n! 定義可知

　　　　　　　1, 當 n=0,
　　　　n! =｛
　　　　　　　n˙(n-1)˙...˙1, 當 n > 0.

以下面的例子為例：
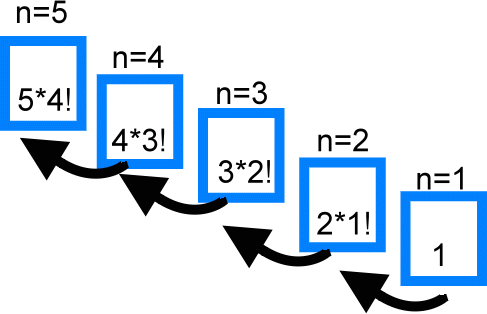
階乘 5!=5*4! 4!=4*3! 3!=3*2! 2!=2*1! 1!=1

Ex.遞迴函式--階乘

#include<stdio.h>
#include<stdlib.h>
int jie_cheng(int n)
{
    if(n==1)
    {
         return 1;
    }

    else
    {
         return n*jie_cheng(n-1);
    }

}

main()
{
printf("%d\n",jie_cheng(5));
system("PAUSE");
}

費氏級數

費波納奇數列是13世紀一個數學家費波納奇發現的.可以用的範圍很多，比方說藝術上的黃金比率，建築設計，甚至艾略特波浪理論(使用費氏級數對股票波動進行分析)，而我們可以使用遞迴來求取答案.

公式如下：fib(n) = fib (n-1) + fib(n - 2)

可以用上表，將月份當成n

fib(1)= 0

fib(2) = 1

fib(3) = fib(2) + fib(1) = 1 + 1 = 2

fib(4) = fib(3) + fib(2) = 2 + 1 = 3

fib(5) = fib(4) + fib(3) = 3 + 2 = 5

fib(6) = fib(5) + fib(4) = 5 + 3 = 8

fib(7) = fib(6) + fib(5) = 8 + 5 = 13

………………以此類推

最大公因數

求最大公因數可以使用輾轉相除法求取，我們可以使用遞迴來求取答案.

同樣的使用遞迴要定義兩件事情:

什麼情況下作遞迴
什麼情況下作遞迴結束

可以知道:

在餘數為0時表示除數為答案.
在餘數不為0時原來的除數為新函式的被除數，而原函式的餘數為新函式除數.

所以GCD(a,b) 定義如下:

當b = 0時傳回a
當b > 0時傳回GCD(b,a%b)

河內塔問題

有三根木樁，在其中一根木樁上放上N個鐵盤，規則是:

一次移動一個鐵盤.
小的鐵盤永遠在大鐵盤的上方.

請問將N個鐵盤全部移動到另一鐵盤需要多少次 ???

設三個木樁為x , y , z,數量為n,函式取名為為Hanoi (n , x , y , z)

當N為1時表示只要再移動一次就完成工作.也就是只要把x移到y就完成工作.
當N不為1時作2個動作.1.執行 Hanoi(n-1,x,z,y); 2.執行Hanoi(n-1,y,x,z);

八皇后問題

在西洋棋裡, 皇后可以在方格盤面上的任意一個方向走任意步. 請問在一個8x8的盤面上, 如何擺上8個皇后, 使她們彼此都吃不到？（表示直、橫、斜線都沒有其他皇后存在。）共有幾種擺法？